

Your good old large suitcase, 30 × 19 × 11 inches or You have to pack your stuff for the three weeks, and you're wondering which suitcase 🧳 will fit more in:
You are going on the vacation of your dreams 🌴.
#Volume of prism how to
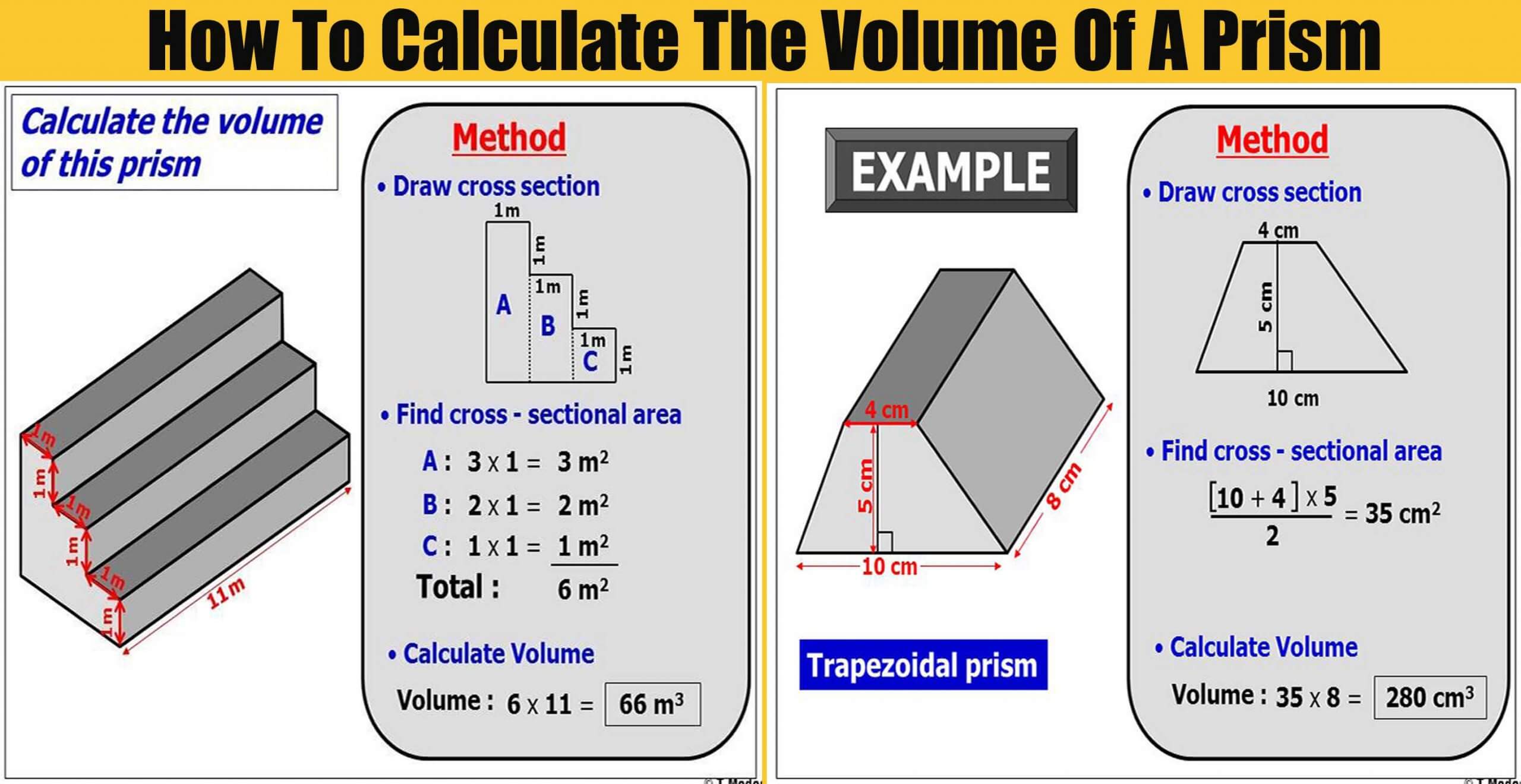
But how much dirt should you buy? Well, that's the same question as how to find the volume of a rectangular prism: measure your raised bed, use the formula, and run to the gardening center. For that, you need to construct a raised bed and fill it with potting soil. The time has come – you've decided that this year you'd like to grow your own carrots 🥕 and salad 🥗. It is a similar story for other pets kept in tanks and cages, like turtles or rats – if you want a happy pet, then you should guarantee them enough living space. If you're wondering how much water you need to fill it, simply use the volume of a rectangular prism formula. It's in a regular box shape, nothing fancy, like a corner bow-front aquarium. You bought a fish tank for your golden fish 🐠. Volume of a pentagonal prism = (0.3) (5) (0.Where can you use this formula in real life? Let's imagine three possible scenarios: NOTE: This formula is only applied where the base or the cross-section of a prism is a regular polygon.įind the volume of a pentagonal prism with a height of 0.3 m and a side length of 0.1 m. S = side length of the extruded regular polygon. The volume of a hexagonal prism is given by:Ĭalculate the volume of a hexagonal prism with the apothem as 5 m, base length as 12 m, and height as 6 m.Īlternatively, if the apothem of a prism is not known, then the volume of any prism is calculated as follows Therefore, the apothem of the prism is 10.4 cmįor a pentagonal prism, the volume is given by the formula:įind the volume of a pentagonal prism whose apothem is 10 cm, the base length is 20 cm and height, is 16 cm.Ī hexagonal prism has a hexagon as the base or cross-section. The apothem of a triangle is the height of a triangle.įind the volume of a triangular prism whose apothem is 12 cm, the base length is 16 cm and height, is 25 cm.įind the volume of a prism whose height is 10 cm, and the cross-section is an equilateral triangle of side length 12 cm.įind the apothem of the triangular prism. The polygon’s apothem is the line connecting the polygon center to the midpoint of one of the polygon’s sides. The formula for the volume of a triangular prism is given as Volume of a triangular prismĪ triangular prism is a prism whose cross-section is a triangle. Let’s discuss the volume of different types of prisms. Where Base is the shape of a polygon that is extruded to form a prism. The volume of a Prism = Base Area × Length The general formula for the volume of a prism is given as Since we already know the formula for calculating the area of polygons, finding the volume of a prism is as easy as pie. The formula for calculating the volume of a prism depends on the cross-section or base of a prism. The volume of a prism is also measured in cubic units, i.e., cubic meters, cubic centimeters, etc. The volume of a prism is calculated by multiplying the base area and the height. To find the volume of a prism, you require the area and the height of a prism. pentagonal prism, hexagonal prism, trapezoidal prism etc. Other examples of prisms include rectangular prism. For example, a prism with a triangular cross-section is known as a triangular prism. Prisms are named after the shapes of their cross-section. By definition, a prism is a geometric solid figure with two identical ends, flat faces, and the same cross-section all along its length.

In this article, you will learn how to find a prism volume by using the volume of a prism formula.īefore we get started, let’s first discuss what a prism is. The volume of a prism is the total space occupied by a prism. Volume of Prisms – Explanation & Examples


 0 kommentar(er)
0 kommentar(er)
